D1.1 Technology survey: Prospective and challenges - Revised version (2018)
3 Water Models
3.2 Data Driven models
The second type of modelling, data-driven, even if it has a similar purpose of connecting one set of output data with the corresponding input set, it is very different in functionality than the physically-based one. It works only with data in the ‘boundaries’ of the domain where data is given. Also, it generates less to none information outside the scope of the model. The model is based on finding different correlations between data sets in order to determine the best input-output pair.
There are several data-driven modelling methods. The most popular of them are presented in the following sub-sections.
Artificial Neural Network (ANN) model
This is one of the most popular data-driven modelling solutions. This paradigm is inspired by the way in which the human brain process information. The model gathers knowledge by detecting relations between data sets and different patterns. An ANN model consists of many artificial neurons or processing units that are connected, forming a complex neural structure. Each processing unit has input sets, a transfer function and one output. The connections between the processing units have a corresponding coefficient or weight. These weights are used as the adjustable parameters of the system. The transfer function determines the behaviour of the network along with the learning rules, and the architecture itself.
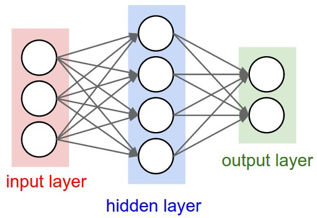
A common neural network model used in many hydroinformatics modelling applications is the Multi-Layer Perceptron (MLP). The MLP network has three different types of layers: input, hidden and output. Figure 3 depicts a single layer fully connected MLP.
Figure 3. Structure of Artificial Neural Network model [Stanford, 2016].
The neural networks are capable of representing any system, even the ones that imply complex, arbitrary and non-linear processes that correlate the input with to output. They are ideal in modelling complex hydrological phenomenon. Paper [Tanty, 2015] presents an analysis of the applications in hydroinformatics modelling that use the MLP model. They divided these applications into four categories: Rainfall-runoff, Stream-Flow, Water Quality and Ground-Water modelling.
Rainfall-runoff Modelling. The first category contains solutions in rainfall-runoff modelling. The modelling applications from this category focused on building virtual hydrological systems, or on predicting monthly rainfall-runoff. The modelling techniques have improved over the years. Thus, in paper [Rajurkar, 2002] the ANN model is combined with multiple-input-single-output (MISO) model in order to have a more accurate representation of the rainfall-runoff relationship for large size catchments. In [Goyal, 2010] is presented an ANN model that uses dimensionless variables. The model analyses the mean monthly rainfall runoff data from several Indian catchments. The results show that this type of modelling is better that the classic ANN model in representing the rainfall-runoff process. In paper [Chen, 2013] the authors presented an ANN model for rainfall-runoff in the context of a typhoon. Other two techniques were used for an accurate interpretation of the results: Feed Forward Backpropagation [Blass, 1992] and Conventional Regression Analysis [Berk, 2004].
Stream-Flow Modelling. Streamflow forecasting is a key element of water systems. It is important especially in the case of critical water resources’ operations for important areas like economy, technology etc. Also, by using this type of forecasting, real-time operations of a specific water resource system can be analysed. There are several articles that present solutions for stream-flow modelling. In papers [Shrivastava, 1999] [Chattopadhyay, 2010] ANN in compared with the Autoregressive Integrated Moving Average (ARIMA) model. In both papers the authors have concluded that ANN produces better results than ARIMA. In papers [Markus, 1995] [Abudu, 2010] the authors present a hybrid modelling solution using ANN with transfer-function noise (TFN) models. The input used were data regarding snow telemetry precipitation and snow water equivalent from the Rio Grande Basin station in Southern Colorado. Their hybrid approach has improved significantly the one-month-ahead forecast accuracy, if compared with simple TFN or ANN models. Also, it has a better generalisation capability than the simple solutions. Another hybrid solution in presented in [Wang (2006)]. The proposed forecasting of daily streamflow model is using three types of hybrid ANN: Threshold-based ANN (TANN), the Cluster-based ANN (CANN), and the Periodic ANN (PANN).
Water Quality Modelling. Lately, the ANN model was used in water quality modelling. Neural Networks are most suited for this type of modelling, as water quality is characterised by a large group of chemical, biological and physical parameters, with complex interactions between them. Paper [Mayer, 1996] demonstrates the efficiency of ANN for this type of complex modelling. The proposed solution was used to estimate the salinity in the River Murray in South Australia. For their solution, the authors designed an ANN model with two hidden layers, and for the training they used a back-propagation function. The input of the model was composed of the following: the daily salinity values, the water levels and flow at upstream stations and at antecedent times. After analysing their results, the authors concluded that their solution could reproduce salinity levels, with the good accuracy, based only on 14 day forecasts. Paper [Zaheer, 2003] presents a decision-making ANN solution for water quality management. This decision making system interprets the input data based on a set of rules. The main objective is to control the environmental pollution. In [Diamantopoulos, 2007] the authors used a Cascade Correlation Artificial Neural Network (CCANN) to determine with accuracy the missing monthly values of water quality parameters mainly in rivers. As case studies, they used input from two rivers near Greek borders: Axios and Strymon River, on which they did a detailed analyse of water quality for a period over 10 years. It has been demonstrated that hybrid modelling solutions can bring improvements in water forecasting. As an example, in the paper [Huiqun, 2008] such a hybrid solution is presented. The authors analyse the of Dongchang lake in Liaocheng city using a combination between ANN and Fuzzy logic.
Ground-Water Modelling. Water quality and ground water modelling are closely related. Ground water is important as a supply resource in different critical areas, such as farming, industrial-based or municipal-based activities. Groundwater level forecasting must be very accurate, as the water level changes periodically. An important analysis regarding the forecasting precision of the ANN models in ground water management is presented in paper [Nayak, 2006]. The model choses the input set that influences most the prediction by using a combination of statistical analysis and domain knowledge. According to the results from this paper, an ANN model is able to forecast the ground water level up to 4 months in advanced with an acceptable precision.
Nearest neighbor model
This model is used mostly in classifications and regressions. It starts from the assumption that nearby points are more likely to be given the same type or same classification that distant ones. An implementation of this model is presented in paper [Buishand, 2001]. The paper presents a multisite generation model of daily precipitation and temperature in a large area using nearest-neighbour resampling. The proposed model efficiency is tested through a set of scenarios such as simulation of extreme precipitation and snowmelt.
Genetic algorithms model
Genetic algorithms (GA) are a subclass of evolutionary algorithms and are based on the Darwinian principles of evolution and natural selection. A genetic algorithm searches for a solution to a problem by evolving a population of individuals towards fitness maximization.
The essential aspects of any genetic algorithm are: representing a solution to the problem as an individual (encoding), evaluating how good an individual is (fitness), and evolving better individuals from the existing ones (selection, crossover). One important advantage of the GA modelling is the possibility of designing simple hydrological models. This is an important feature, as most of the data driven modelling solutions are too complex, thus the user cannot easily determine what is happening during the model computation. Several solutions have been proposed for GA water modelling (e.g. [Ghorbani, 2010], [Sreekanth, 2012])
Fuzzy rule based system model
Systems based on Fuzzy logic can work with highly variable, vague and uncertain data and are frequently used in decision-making as they provide a logical and transparent stream processing from data collection down to data usage. And thus they are ideal in modelling the complex hydrological events.
In the artificial neural network section, we presented different type of hydrological models, such as rainfall–runoff modelling applications. This type of applications has a non-linear behaviour and is affected by a large variety of external factors. For example, for the rainfall–runoff modelling we have factors such as rainfall characteristics, soil moisture, watershed morphology and so on. And, although the ANN provides accurate results, it has a black box approach. Lately, the research has focus on this black box characteristic by designing semantic-based fuzzy neural architecture, a combination between ANN and fuzzy logic. Such a solution is presented in paper [Talei, 2010]. The authors present a detailed analyse of Adaptive Network-based Fuzzy Inference Systems (ANFIS) in rainfall–runoff modelling. They have implemented and tested15 different ANFIS models.
Decision/model tree model
In this model the instances are classified by sorting them up the “tree” from the “root” to some “leaf” node that provides a classification of the instance. Each node tree specifies a test of some attribute of the instance, and each branch descending from a node corresponds to one of the possible values for this attribute. An instance is classified by starting at the root node of the tree, testing the attribute specified by this node, the moving down the branch corresponding to the value of the attribute. This process is repeated for the sub-tree root based at the new node.
Support vector machine model
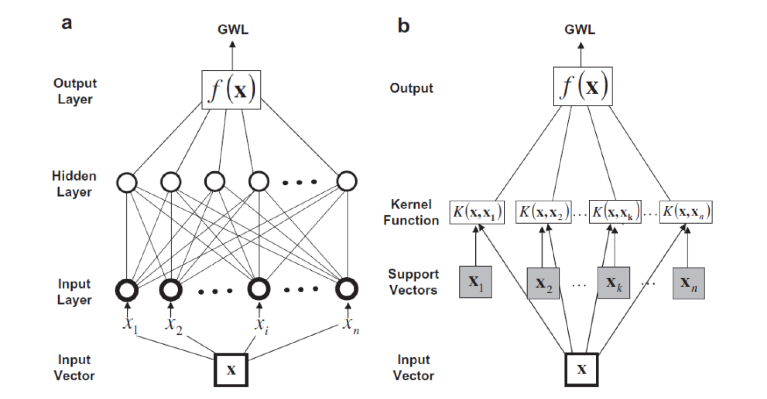
SVM is a learning system and it is based on statistical learning theory [Vapnik, 1998]. A specific characteristic of SVM is that its structure is not determined a priori. It uses an approximation function (kernel function) that is chosen based on how well it fits the verification and the training set using statistical learning theory. A comparison between ANN and SVM is done in paper [Yoon, 2011].
Figure 4. Schematic diagram for (a) ANN and (b) SVM [Yoon, 2011].